How Bond Portfolios Lose Money & Bounce Back

In this commentary, we explore the underlying mechanics of what goes on inside a bond fund and how its price changes over time if interest rates experience a one-time increase.

I. Introduction

Interest rates are at historic lows, and while at the beginning of 2010 it seemed that interest rates could only go higher, they actually fell even more. The 10 Year US Treasury (the bond that most mortgage loans are related to) yielded ~2.5% on September 30, 2010. Since bond values increase when interest rates fall and decrease when rates rise, an investor in a bond fund will lose money in the short term when interest rates rise. However, a bond fund investor will actually recover those losses from a one-time increase in interest rates in a fairly short period of time and in the intermediate term start earning a higher rate of return.

II. Bond Funds Are Just a Bunch of Bonds

A popular technique for investing in bonds is called “laddering.” Using this technique, an investor buys bonds that mature at equal intervals in the future. A “10 year annual bond ladder” has bonds maturing each year for 10 years. With the passage of one year, all the bonds become one year closer to maturity (i.e., the 10 year bond becomes due in nine years). The shortest term bond matures, and the investor reinvests the proceeds from the matured bonds and the coupons received in another bond due 10 years from investment. (This reinvestment assumes the investor doesn’t spend any money.) If interest rates remain the same, the return on the bonds is equal to the coupon rate on the bonds.

A mutual fund is an investment company that holds securities. Mutual funds can be useful to individual investors by allowing them to benefit from economies of scale, thereby realizing lower trading costs, benefits of professional management, and liquidity. Owning a bond fund is like owning a proportional interest in a bunch of bonds. As long as the investor understands the nature of the bonds owned by the fund, bond funds can be easily incorporated in an investment strategy. Understanding how the price of a bond fund changes is the same as understanding how changes in interest rates affect the price of a bunch of bonds.

III. Bond Pricing – A Primer

To understand how interest rates affect a bunch of bonds, we first need to understand how to value a single bond. A bond holder pays a certain amount of money in return for receiving coupon payments and return of principal at times certain. To keep things simple, we assume that the bond holder pays a certain amount of money for a bond in return for $1 (equivalent to 1% annual coupon) at the end of every year for five years and $100 at maturity (the end of year five). The value of this bond to the investor is the discounted value of the stream of future payments (the coupons and bond principal paid at maturity). If interest rates were 1%, then this bond would be worth $100.

But what if interest rates increased to 2%? The value of the bond would still be the discounted value of the same stream of future payments, but this value would be lower since the discount rate is higher. The bond value would actually fall to $95 — a 5% loss!

Another way to think of this loss is that if you have ever purchased something that went on sale the next day by 10%, you could have spent 10% less money if you had waited a day. Purchasing the item the day before the sale leads to a 10% loss. The change in price of a bond depends on the duration of the bond. The longer a bond is outstanding, the greater the sensitivity to changes in interest rates.

IV. A Simple Bond Portfolio Example

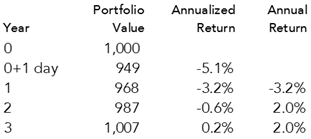
Now let’s assume that the investor owns a bunch of bonds as described in Section II above. The cash flows for this portfolio are shown in the figure below. The coupons collected in year one are $1 on each of the 10 bonds held, or $10 total. The value of this bond portfolio is $1,000, assuming an interest rate of 1%.

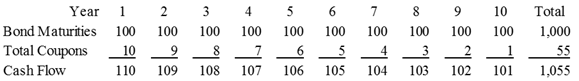
The value of this bond portfolio is $1,000, assuming an interest rate of 1% and the duration is a little over 5 years (taking into account the timing of the payments of principal and interest).

A. Bonds Go On Sale!!!

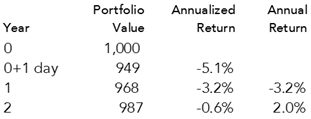
On the day after the investor purchases the 10 bonds for $1,000, the interest rate in the market doubles from 1% to 2%. The value of the original 10 bonds falls to $950, a 5% loss.

B. One Year Gone By

After stomaching the losses on day one, the investor stays the course until the end of the first year when one bond matures and $10 in coupons are paid. This money ($110) is used to buy another 10 year bond at the current rate of 2%. The total coupons have increased due to the higher interest rate on this new bond and the reinvestment of the coupons themselves.

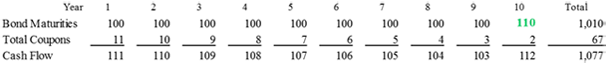
The value of the portfolio has also increased from the day one fall since the cash flows from the portfolio have grown. The loss for the first year is now -3.2%.

C. Another Year Gone By

Another year goes by with no change in interest rates. Another bond matures, and coupons totaling $11 are paid. This money ($111) is used to buy another 10 year bond at the current rate of 2%. The total coupons have increased again for the same reasons as before.

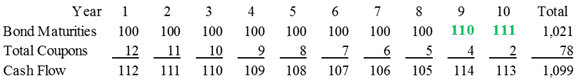
The value of the portfolio has also continued to grow to $987 since the cash flows from the portfolio have grown again. The portfolio gains 2% — equal to the current rate of interest. The cumulative loss is now only -0.6% per year.

D. Recovery in the Third Year

During the third year, interest rates remain at 2% and the maturing bond is invested at the current rate. Since the portfolio returns 2%, its value has now recovered to $1,007, greater than the amount originally invested.

E. Redemption by the Fifth Year

In this scenario, interest rates remain the same, coupons and bond maturities are reinvested, and by the end of the fifth year the cumulative return on the portfolio is almost 1%.

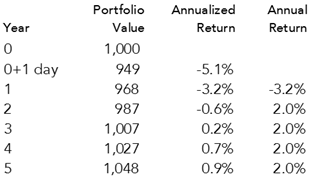
This return is significant because the bond portfolio has earned almost exactly the same return as was originally expected (i.e., 1%). For every year thereafter, the annualized geometric return will be higher than the expected return when the bonds were originally purchased.

F. So What Did This Example Show?

There are a few short take-aways from this example:

1. The initial increase in interest rates is painful.
2. The portfolio recovers in two years (if coupons and bond maturities are reinvested).
3. The portfolio starts profiting from the increase in rates in five years (and making even more income than originally anticipated after that).

For an investor with a ten year bond portfolio and a time horizon longer than five years, the impact of the increase in interest rates is actually positive. These conclusions are reliant on the assumptions in the example.

V. So Now What?

We recommend that long term investors hold bonds in their portfolios to counterbalance the risk of equity investments. Fixed income (bonds) should also be used to match known future spending. While changes in interest rates will not likely prevent the bonds from earning their expected return, considered in isolation, other factors could influence the return, including credit risk and liquidity.

We also expect interest rates and equity returns to be linked. If interest rates rise, it is usually due to increased economic activity that has driven stock returns higher. The corollary is also usually true – e.g., interest rates fell significantly during the recent period of economic crisis and slowdown. In this era of high government deficits, interest rates could increase due to other factors not related to the economy in a stagnant stock market environment. We are concerned about this scenario since the counterbalancing of risk between bonds and stocks may not work as intended when interest rates rise while the stock market remains flat. We do not, however, think that long term investors should be overly concerned about increases in interest rates. While painful in the short term, rising interest rates eventually lead to higher returns.

---